Filosofa.net

Полученное нами вероятностное описание несводимо: это неизбежное следствие того, что собственные функции принадлежат к классу обобщенных функций. Как уже упоминалось, этот факт можно использовать в качестве отправного пункта нового, более общего определения хаоса. В классической динамике хаос определяется "экспоненциаль­ным разбеганием"[1] траекторий, но такое определение хаоса не допускает обобщения на квантовую теорию. В квантовой теории нет "экспоненциального разбегания" волновых функций и, следовательно, не существует чувствительности к началь­ным условиям в обычном смысле. Тем не менее, существуют квантовые системы, характеризующи­еся несводимыми вероятностными описаниями. Помимо прочего такие системы имеют принципиальное значение для нашего описания при­роды. Как и прежде, фундаментальные законы физики применительно к таким системам формулируются в виде вероятностных утверждений (а не в терминах волновых функций). Можно сказать, что такие системы не позволяют отличить чистое состояние от смешанных состояний. Даже если мы выберем в качестве исходного, чистое состояние, оно со временем превратится в смешанное состояние.

Исследование описанных в этой главе отображений представляет большой интерес. Эти простые примеры позволяют наглядно предста­вить, что мы имеем в виду, говоря о третьей, несводимой, формулировке законов природы. Тем не менее, отображения — не более чем абстракт­ные геометрические модели. Теперь же мы обратимся к динамическим системам на основе гамильтонова описания — фундамента современ­ной концепции законов природы.

5.2.Квантовый хаос

Квантовый хаос отождествляется с существованием несводимого вероятностного представления. В случае с БСП в основе такого представления лежат резонансы Пуанкаре.

Следовательно, квантовый хаос связан с разрушением инварианта движения вследствие резонансов Пуанкаре. Это свидетельствует о том, что в случае БСП невозможно переходить от амплитуд |φi+> к вероятностям |φi+> <φi+|. Фундаментальное уравнение в данном случае записывается в терминах вероятности. Даже если начать с чистого состояния ρ=|ψ> <ψ|, оно разрушится в ходе движения системы к равновесию.

Разрушение состояния может быть связано с разрушением волновой функции. В данном случае эволюция "коллапса" настолько важна, что имеет смысл проследить ее на примере[1, 178].

Пусть существует волновая функция ψ(0) в некоторый начальный момент времени t=0. Уравнение Шредингера преобразует ее в ψ(t)=

e-itHψ(0). Всякий раз, когда приходится иметь дело с несводимыми представлениями, выражение ρ=ψψ[3] должно утрачивать смысл, иначе было бы возможно переходить от ρ к ψ и наоборот.

Именно это и происходит с неисчезающими взаимодействиями в потенциальном рассеянии.

На рис.1 отражены графики зависимости sin(ώt)/ώ от ώ

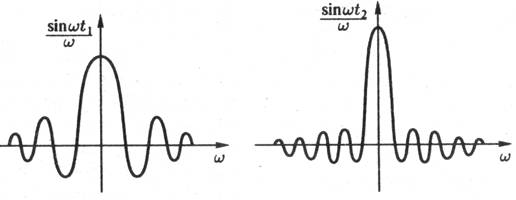
рис.1 Схематический график величины sin(ώt)/ώ

Имея волновую функцию можно вычислить матрицу плотности

.

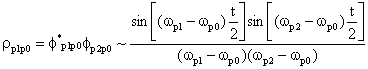Это выражение плохо определено, но в сочетании с пробными функциями оба плохо определенных выражения имеют смысл:

Рассмотрим диагональные элементы матрицы плотности:

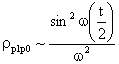
График этой функции приведен на рис.2

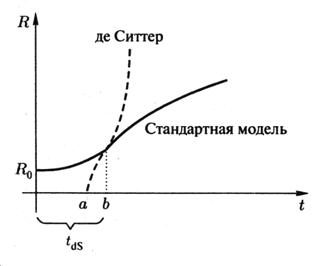
рис. 2 схематический график величины

В сочетании с пробной функцией f(ω) требуется вычислить

И наоборот, амплитуда волны в сочетании с пробной функцией остается постоянной во времени, т.к.

.

Причина столь различного поведения функций становится ясной если сравнить графики функций приведенных на рис.1 и 2: функция sinωt/ω принимает как положительные, так и отрицательные значения, тогда как функция принимает только положительные значения и дает "более больший вклад в интеграл"[1, 180].

Полученные заключения могут быть подтверждены моделированием вероятности Р как функции от k при возрастающих значениях t. Графики приведены на рис.5[5, 241].

Теперь можно отметить, что коллапс распространяется в пространстве причинно, в соответствии с общими требованиями теории относительности, исключающими эффекты распространяющиеся мгновенно[1, 181].

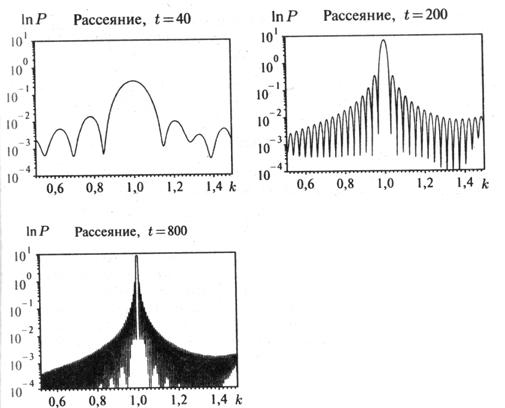
рис. 3 моделирование вероятности P как функции от k при возрастающих значениях t.

Кроме того, для достижения равновесия за конечное время, рассеяние должно неоднократно повторится, т.е. необходимы системы N тел с непрекращающимися взаимодействиями[2].

5.3.Хаос и законы физики

Хаос неоднократно определялся через существование несводимых вероятностных представлений. Такое определение позволяет охватить гораздо более широкую область, чем первоначально предполагали основатели современной динамической теории хаоса, в частности, А. Н. Колмогоров и Я. Г. Синай. Хаос обусловлен чувствительностью к начальным условиям и, следовательно, экспоненциальным разбеганием траекторий. Это приводит к несводимым вероятностным представлениям. Описание в терминах траекторий уступило место вероятностному описанию. Следовательно, можно принять это фундаментальное свойство за отличительную особенность хаоса. Развивается неустойчивость, которая вынуждает нас отказаться от описания в терминах отдельных траекторий или отдельных волновых функций.

Существует принципиальное различие между классическим хаосом и квантовым хаосом. Квантовая теория непосредственно связана с волновыми свойствами. Постоянная Планка приводит к дополнительной по сравнению с классическим поведением когерентности. В результате условия для квантового хаоса становятся более ограниченными, чем условия для классического хаоса[2]. Классический хаос, возникает даже в малых системах, например, в отображенной и системах, исследуемых теорией КАМ. Квантовый аналог таких малых систем обладает квазипериодическим поведением. Многие авторы пришли к заключению, что квантового хаоса вообще не существует. Но это не так. Во-первых, требуется, чтобы спектр был непрерывным (т. е. чтобы квантовые системы были «большими»). Во-вторых, квантовый хаос определяется как связанный с возникновением несводимых вероятностных представлений[1].

Традиционная квантовая теория имеет большое число слабых мест. Формулировка этой теории продолжает традицию классической теории — в том смысле, что следует идеалу вневременного описания. Для простых динамических систем, таких как гармонический осциллятор, это вполне естественно. Но даже в этом случае можно ли описывать такие системы изолированно? Их невозможно наблюдать в отрыве от поля, приводящего к квантовым переходам и испусканию сигналов (фотонов)[5].

Чтобы включить в картину эволюционные элементы, необходимо перейти к формулировке законов природы в терминах несводи­мого вероятностного описания.

6.Теория неустойчивых динамических систем – основа космологии

Космология должна опираться на теорию неустойчивых динамических систем. В какой-то мере это всего лишь программа, но, с другой стороны, в рамках физической теории она существует в настоящее время.

Кроме того, введение вероятности на фундаментальном уровне устраняет некоторые препятствия на пути к построению последовательной теории гравитации. В своей работе Унру и Вальд писали, что указанная трудность может быть прослежена непосредственно до конфликта между ролью времени в квантовой теории и природой времени в общей теории относительности. В квантовой механике все измерения производятся в "моменты времени": физический смысл имеют только величины, относящиеся к мгновенному состоянию системы. С другой стороны, в общей теории относительности измерима только геометрия пространства-времени. Действительно, как мы видели, квантовая теория измерений соответствует мгновенным, акаузальным процессам. С точки зрения авторов, это обстоятельство является сильным аргументом против «наивной комбинации» квантовой теории и общей теории относительности, включающей в себя и такое понятие, как «волновая функция Вселенной». Но, такой подход позволяет избежать парадоксов, связанных с квантовыми измерениями.