Реклама
Рефераты по философии
Моделирование, как необходимый научный метод познания
С О Д Е Р Ж А Н И Е
|
ВВЕДЕНИЕ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 3 | |
| 1. |
МОДЕЛИРОВАНИЕ КАК НЕОБХОДИМЫЙ ЭТАП ПОЗНАНИЯ СУЩНОСТИ ИЗУЧАЕМОГО ЯВЛЕНИЯ ИЛИ ПРО-ЦЕССА ПРИ РАЗРАБОТКЕ ЕГО ТЕОРИИ . . . . . . . . . . . . . . . . . . |
4 |
| 2. |
ГИПОТЕЗЫ КАК НЕОБХОДИМЫЕ ПРИЗНАКИ, ОПРЕДЕ-ЛЯЮЩИЕ СВОЙСТВА РАЗРАБАТЫВАЕМОЙ МОДЕЛИ ИЛИ ПРОЦЕССА . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
8 |
| 3. |
ПРЕДСКАЗАНИЯ — ВАЖНЕЙШИЙ КРИТЕРИЙ ИСТИН-НОСТИ РАЗРАБАТЫВАЕМОЙ ТЕОРИИ . . . . . . . . . . . . . . . . . . . | 15 |
| 4. |
ПРИМЕНЕНИЕ РАЗРАБОТАННОЙ ТЕОРИИ К ПРАКТИ-ЧЕСКИМ ЗАДАЧАМ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 16 |
| 5. |
СВЯЗЬ МОДЕЛИРОВАНИЯ С ДЕТЕРМИНИРОВАННЫМИ И СТОХАСТИЧЕСКИМИ МЕТОДАМИ ИЗУЧЕНИЯ ЯВЛЕ-НИЯ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 17 |
|
ЗАКЛЮЧЕНИЕ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 19 | |
|
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ . . . . . . . . . . . . . . . . . | 20 | |
В В Е Д Е Н И Е
Бурный рост промышленности и науки во всех сферах человеческой деятельности привели в настоящее время к такому положению вещей, что создание и разработка каких-либо новых технологий, технических средств (машин, приборов, оборудования и т. п.), а также методик их применения для нужд человека становится затруднительным, а в некоторых случаях невозможным, без интенсивного применения научных методов познания и поиска [2].
Одной из таких обязательных сторон научного исследования является метод моделирования, без которого не обходится ни одна конструкторская и ни одна исследовательская работа. По этой причине, в реферате сделан значительный акцент на метод моделирования как необходимый научный метод познания явлений природы и использование этого познания для практических целей [4].
1. МОДЕЛИРОВАНИЕ КАК НЕОБХОДИМЫЙ ЭТАП
ПОЗНАНИЯ СУЩНОСТИ ИЗУЧАЕМОГО ЯВЛЕНИЯ
ИЛИ ПРОЦЕССА ПРИ РАЗРАБОТКЕ ЕГО ТЕОРИИ
Всякое вновь изучаемое явление или процесс бесконечно сложно и многообразно и потому до конца принципиально не познаваемо и не изучаемо. Поэтому, приступая к изучению явления или процесса, исследователь заменяет его схематической моделью, которая выбирается тем более сложной, чем подробнее и точнее нужно изучить упомянутое явления. В моделе сохраняется только самые существенные стороны изучаемого явления, а все мало существенные свойства и закономерности отбрасываются [6].
Какие стороны изучаемого явления необходимо сохранить в модели и какие отбросить, зависит от постановки задачи исследований. Цель и задачи исследований формулируются перед началом разработки теории еще неизученного явления или уточнения уже существующей теории с целью более адекватного описания изучаемого процесса или явления [7]. Построение теории начинается с выбора некоторого достаточного множества понятий и определения тех объектов, с которыми будет оперировать формируемая теория. Иногда список исходно определяемых понятий и объектов называют терминами теории. Они должны быть определены так, чтобы воспринимались любым исследователем однозначно.
Далее необходимо ввести, при построении модели явления, самые необходимые свойства определяемых объектов (“кирпичей” теории) и правила их взаимодействия и преобразования. Список введенных свойств и правил должен быть полным, т. е. таким, оперируя с которым можно осуществить любое действие по решению поставленных в исследовании задач и доведения решения логического и однозначного результата. Указанный список должен быть логически непротиворечивым, иначе создаваемая теория приведет к ошибочным заключениям. Вводимые правила должны быть выполнимы, а результаты их использования однозначными и определенными.
Выделенное множество объектов-терминов теории и правил их преобразования должно допускать проверку практикой или иными надежными методами. При этом выбранная модель должна обеспечивать необходимую точность результатов [6].
В философском смысле дать определение некоторому понятию-термину — это значит подвести более узкое определяемое понятие или подпонятие под более широкого и указать отличительную особенность. Это означает, что, давая определения вводимым в теорию терминам, мы определяем их в конце концов через ряд неопределимых исходных понятий. Тем самым становится возможным неоднозначное толкование, которое позволяет прилагать сформулированную теорию к любым явлениям, имеющим в своей основе аналогичные структуры исходных понятий.
Так, например, в курсе геометрии в разделе планиметрия понятие точки не вводится, а понятие отрезок прямой o-b вводится как континуальное множество точек — последовательность точек c, ведущих из начальной точки отрезка o к конечной точке b, имеющее наименьшую длину
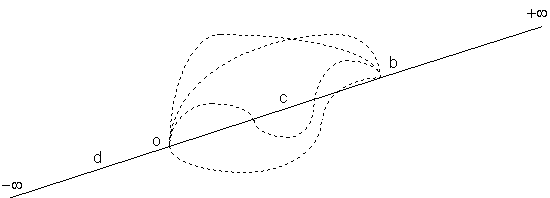
Рис. 1
Путем продолжения отрезка в направлении от точки d к с получаем полупрямую, а продолжая отрезок и в противоположную сторону от точки d, будем иметь бесконечную прямую(рис. 1).
В дальнейшем, точки рассматриваются как места пересечения линий.
Рассмотрим проективные модели Римана: проведем через точку o прямой перпендикуляр (рис. 2), на котором отметим точку o p, на отрезке o-o p, как на диаметре, построим окружность, касающуюся прямой в точке o. Точку o назовем полюсом.
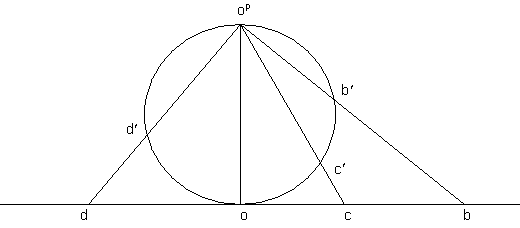
Рис. 2
Соединим полюс с точками d, c и b, каждая из приведенных проектирующих прямых пересекает окружность в точках d ¢, c ¢ и b ¢. Очевидно, между точками d и d ¢, c и c ¢, b и b ¢, имеется взаимооднозначное соответствие. Полюс o pвзаимооднозначно соответствует бесконечно удаленной точке прямой. Как видно в проективной модели Римана имеется образ одной бесконечно удаленной точки прямой — это точка, совпадающая с полюсом o p, в то время как на рис. 1 могло показаться, что прямая обладает двумя бесконечно удаленными точками. В развитие этой модели приведем проективную модель Римана для сферы и плоскости N.
Возьмем плоскость N, в точке o которой поместим сферу диаметром o-o p. Рассматривая точку o pкак полюс проектирования, спроектируем

Рис. 3
прямыми, проходящими через полюс o p, расположенные в плоскости N, то точки d, c, b на поверхность сферы в виде точек-образов d ¢, c ¢, b ¢. Как и в линейном случае (рис. 2) между точками d, c, b и их проективными образами d ¢, c ¢, b ¢ имеется взаимно однозначное соответствие. Доказывается, что при таком проективном преобразовании сохраняются углы между линиями d, c, b на плоскости и линиями d ¢, c ¢, b ¢ на поверхности сферы. Рассмотренное проектированное преобразование служит теоретическим основанием для изображения карты земной поверхности на плоскости N и широко используется в навигации, в морском и авиационном штурманском деле. Полюс проектирования o p по Риману, также как и в линейном случае (рис. 2), является проективным образом бесконечно удаленной точки плоскости. Риманова модель дает основание считать, что плоскость содержит не множество бесконечно удаленных точек, а только одну. Такой подход дает большие удобства для математических построений в теории функции комплексного переменного и в прикладных задачах.
Название: Моделирование, как необходимый научный метод познания
Дата: 2007-06-07
Просмотрено 9936 раз