Реклама
Рефераты по философии
Великие законы сохранения
СОДЕРЖАНИЕ
Сохраняющиеся величины . 3
Закон сохранения импульса . 3
Энергия и работа . 6
Консервативные силы . 8
Потенциальная энергия . 8
Закон сохранения энергии .9
Закон сохранения момента импульса 11
Список используемой литературы 16
СОХРАНЯЮЩИЕСЯ ВЕЛИЧИНЫ
Совокупность тел, выделенных для рассмотрения, называется механической системой. Тела системы могут взаимодействовать как между собой, так и с телами, не входящими в систему. В соответствии с этим силы, действующие на тела системы, подразделяются на внутренние и внешние. Внутренними называют силы, с которыми тела системы действуют друг на друга, внешними - силы, обусловленные воздействием тел, не принадлежащих системе. Система, в которой внешние силы отсутствуют, называется замкнутой.
Для замкнутых систем остаются постоянными (сохраняются) три физические величины: энергия, импульс и момент импульса. Соответственно имеются три закона сохранения: закон сохранения энергии, закон сохранения импульса и закон сохранения момента импульса. Эти законы тесно связаны со свойствами времени и пространства.
Кроме названных, есть еще ряд законов сохранения (например, закон сохранения электрического заряда). Законы сохранения являются фундаментальными законами природы.
Рассматриваемые в механике законы сохранения энергии, импульса и момента импульса оказываются точными законами и имеют всеобщий характер - они применимы не только к механическим явлениям, но и вообще ко всем явлениям природы, в частности они соблюдаются в релятивистской области и в мире элементарных частиц.
Законы сохранения не зависят от природы и характера действующих сил. Поэтому с их помощью можно делать ряд важных заключений о поведении механических систем даже в тех случаях, когда силы остаются неизвестными.
ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
Рассмотрим систему, состоящую из N частиц (материальных точек). Обозначим через Fik силу, с которой k-я частица действует на i-ю (первый индекс указывает номер частицы, на которую действует сила, второй индекс - номер частицы, воздействием которой обусловлена эта сила). Символом Fi обозначим результирующую всех внешних сил, действующих на i-ю частицу. Напишем уравнения движения всех N частиц:
![]() =F12 + F13 + . + F1k + . + F1N + F1=
=F12 + F13 + . + F1k + . + F1N + F1=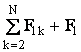 ,
,
![]() =F21 + F23 + . + F2k + . + F2N + F2=
=F21 + F23 + . + F2k + . + F2N + F2=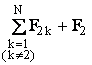 ,
,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
![]() =Fi1 + Fi2 + . + Fik + . + FiN + Fi =
=Fi1 + Fi2 + . + Fik + . + FiN + Fi =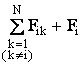 ,
,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
![]() =FN1 + FN2 + . + FNK + . +FN,N-1 + FN =
=FN1 + FN2 + . + FNK + . +FN,N-1 + FN =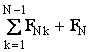
(pi – импульс i-й частицы).
Сложим вместе эти уравнения. Слева получиться производная по времени от суммарного импульса системы:
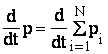 .
.![]()
Справа отличной от нуля будет только сумма внешних сил Fi. Действительно, сумму внутренних сил можно представить в виде
(F12+F21) + (F13 + F31) + . + (Fik + Fki) + . + (FN-1,N + FN,N-1).
Согласно третьему закону Ньютона каждая из скобок равно нулю. Следовательно, сумма внутренних сил, действующих на тела системы, всегда равна нулю:
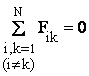 .
.
С учетом этого получим, что
![]() . (1)
. (1)
Таким образом, производная по времени от суммарного импульса системы равна сумме внешних сил, действующих на тела системы.
Если система замкнута, внешние силы отсутствуют и правая часть уравнения (1) равна нулю. Соответственно dp/dt=0 и, следовательно, p=const.
Итак, мы пришли к выводу, что суммарный импульс замкнутой системы материальных точек остается постоянным. Это утверждение составляет содержание закона сохранения импульса.
В основе закона сохранения импульса лежит однородность пространства, т.е. одинаковость свойств пространства во всех точках. Параллельный перенос замкнутой системы из одного места в другое без изменения взаимного расположения и скоростей частиц не изменяет механических свойств системы. Поведение системы на новом месте будет таким же, каким оно было бы на прежнем месте.
Заметим, что согласно формуле (1) импульс остается постоянным и у незамкнутой системы в том случае, если сумма всех внешних сил равна нулю.
Спроектировав все векторы, фигурирующие в уравнении (1), на некоторое направлениеx, получим
![]() (2)
(2)
(![]() ; отсюда следует, что проекция на ось x вектораp равна dpx/dt). Согласно (2) для того, чтобы сохранялась проекция суммарного импульса на некоторое направление, достаточно равенства нулю проекции на это направление суммы внешних сил; сама эта сумма может быть отличной от нуля.
; отсюда следует, что проекция на ось x вектораp равна dpx/dt). Согласно (2) для того, чтобы сохранялась проекция суммарного импульса на некоторое направление, достаточно равенства нулю проекции на это направление суммы внешних сил; сама эта сумма может быть отличной от нуля.
Точка С, положение которой определяется радиус-вектором
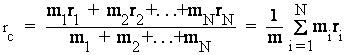
называется центром масс системы материальных точек. Здесь mi – масса i-й частицы, ri – радиус-вектор, задающий положение этой частицы, m – суммарная масса системы. Отметим, что в однородном поле сил тяжести центр масс совпадает с центром тяжести системы.
Спроектировав rc на координатные оси, получим декартовы координаты центра масс:
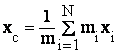 ,
, 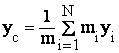 ,
, 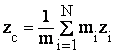 .
. ![]()
Продифференцировав rc по времени, найдем скорость центра масс:
 (3)
(3)
Согласно (3) суммарный импульс системы можно представить в виде произведения массы системы на скорость центра масс:
p=mVc
Подставив это выражение в формулу (1), получим уравнение движения центра масс:
![]()
![]()
(ас - ускорение центра масс). Таким образом, центр масс движется так, как двигалась бы материальная точка с массой равной массе системы, под действием результирующих всех внешних сил, приложенных к телам системы. Для замкнутой системы ас=0. Это означает, что центр масс замкнутой системы движется прямолинейно и равномерно, либо покоится.
Система отсчета, относительно которой центр масс покоится, называется системой центра масс (сокращенно ц-системой). Эта система инерциальна. Система отсчета, связанная с измерительными приборами, называется лабораторной системой (сокращенно л-системой).
Энергия и работа
Энергия - это запас работы системы. Энергия является общей количественной мерой движения и взаимодействия всех видов материи. Энергия не исчезает и не возникает из ничего, она может лишь переходить из одной формы в другую. Понятие энергии связывает воедино все явления природы. В соответствии с различными формами движения материи рассматривают различные виды энергии: механическую, внутреннюю, электромагнитную, ядерную и др.
Название: Великие законы сохранения
Дата: 2007-06-10
Просмотрено 22613 раз